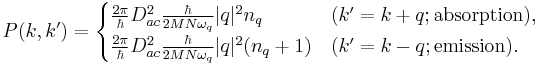Electron-longitudinal acoustic phonon interaction
Electron-longitudinal acoustic phonon interaction is an equation concerning atoms.
Contents |
Displacement operator of the longitudinal acoustic phonon
The equation of motions of the atoms of mass M which locates in the periodic lattice is
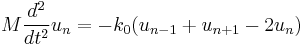 ,
,
where 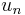 is the displacement of the nth atom from their equilibrium positions.
is the displacement of the nth atom from their equilibrium positions.
If we define the displacement 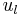 of the nth atom by
of the nth atom by 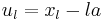 , where
, where 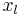 is the coordinates of the lth atom and a is the lattice size,
is the coordinates of the lth atom and a is the lattice size,
the displacement is given by 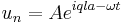
Using Fourier transform, we can define
and
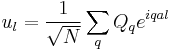 .
.
Since 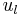 is a Hermite operator,
is a Hermite operator,
From the definition of the creation and annihilation operator 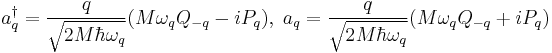
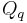 is written as
is written as
Then 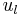 expressed as
expressed as
Hence, when we use continuum model, the displacement for the 3-dimensional case is
![u(r) = \sum_{q} \sqrt{ \frac {\hbar}{2M N \omega_{q} } } e_{q} [ a_{q} e^{ i q \cdot r} %2B a^{\dagger}_{q} e^{-i q \cdot r} ]](/2012-wikipedia_en_all_nopic_01_2012/I/9997c7347a37e71c8caa1ca5a6df1be6.png) ,
,
where 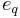 is the unit vector along the displacement direction.
is the unit vector along the displacement direction.
Interaction Hamiltonian
The electron-longitudinal acoustic phonon interaction Hamiltonian is defined as 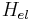
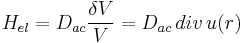 ,
,
where 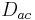 is the deformation potential for electron scattering by acoustic phonons.[1]
is the deformation potential for electron scattering by acoustic phonons.[1]
Inserting the displacement vector to the Hamiltonian results to
Scattering probability
The scattering probability for electrons from 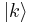 to
to 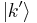 states is
states is
Replace the integral over the whole space with a summation of unit cell integrations
where 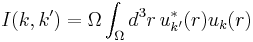 ,
,  is the volume of a unit cell.
is the volume of a unit cell.
Notes
- ^ Hamaguchi 2001, p. 208.
References
- C. Hamaguchi (2001). Basic Semiconductor Physics. Springer. pp. 183–239.
- Yu, Peter Y. and Cardona, Manuel (2005). Fundamentals of Semiconductors (3rd ed.). Springer.
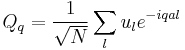
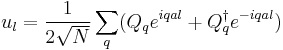
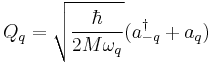
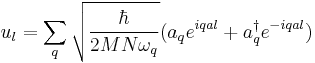
![H_{el} = D_{ac} \sum_{q} \sqrt{ \frac {\hbar} {2 M N \omega_{q} } } ( i e_{q} \cdot q ) [ a_{q} e^{i q \cdot r} - a^{\dagger}_{q} e^{-i q \cdot r} ]](/2012-wikipedia_en_all_nopic_01_2012/I/c10cae2663c0f46a4d960fc1cb29d761.png)
![P(k,k') = \frac {2 \pi} {\hbar} \mid \langle k' , q' | H_{el}| \ k , q \rangle \mid ^ {2} \delta [ \varepsilon (k') - \varepsilon (k) \mp \hbar \omega_{q} ]](/2012-wikipedia_en_all_nopic_01_2012/I/7c63fe0c3518b623539a44e4fc4ab024.png)
![= \frac {2 \pi} {\hbar} \left| D_{ac} \sum_{q} \sqrt{ \frac {\hbar} {2 M N \omega_{q} } } ( i e_{q} \cdot q ) \sqrt { n_{q} %2B \frac {1} {2} \mp \frac {1} {2} } \, \frac {1} {L^{3}} \int d^{3} r \, u^{\ast}_{k'} (r) u_{k} (r) e^{i ( k - k' \pm q ) \cdot r } \right|^2 \delta [ \varepsilon (k') - \varepsilon (k) \mp \hbar \omega_{q} ]](/2012-wikipedia_en_all_nopic_01_2012/I/2d515cd0b5144894bb926e9a2e46a166.png)
![P(k,k') = \frac {2 \pi} {\hbar} \left( D_{ac} \sum_{q} \sqrt{ \frac {\hbar} {2 M N \omega_{q} } } | q | \sqrt { n_{q} %2B \frac {1} {2} \mp \frac {1} {2} } \, I(k,k') \delta_{k' , k \pm q } \right)^2 \delta [ \varepsilon (k') - \varepsilon (k) \mp \hbar \omega_{q} ],](/2012-wikipedia_en_all_nopic_01_2012/I/d0ba47a4aa63369a42f370414280adb5.png)